Image Database Browsing
This approach is described in the ICPR'02 paper that can be found in the publication page.
Abstract:
- Introduction
- Background
- Adaptive Robust Competition (ARC)
- Dimensionality Reduction
- Adaptive Competition
- Robust clustering
- Choice of distance for good clusters
- Normalization of features
- Algorithm outline
- Results and discussion
- Conclusion
- Bibliography
Introduction
Content-based Image Retrieval (CBIR) aims at indexing images by automatic description, which only depends on their objective visual content. The purpose of browsing is to help user to find his target by providing first the best overview of the database. We propose to categorize the database and then to choose a key image for each category. This summary can be used as an initial overview.
The categorization is performed in the image signature space. The main issues of the problem are the high dimensionality of this feature space, the unknown number of natural categories in the data, and the variety and the complexity of these categories, which are often overlapping.
A popular way to find partitions in complex data is to use prototype-based clustering algorithms. The fuzzy version (Fuzzy C-Means [1]) has been constantly improved for twenty years, by the use of the Mahalanobis distance [6], the adjunction of a noise cluster [3] or the competitive agglomeration algorithm [5] [2]. Specific algorithms have been developed for the categorization [8] [4] and the browsing [11] of image databases.
This paper is organized as follows. §2 presents the background of our work. Our method is presented in §3. The results on image databases are discussed and compared with other clustering methods in §4, §5 summarizes our concluding remarks.
Background
The Competitive Agglomeration (CA) algorithm [5] is a fuzzy partitional algorithm which does not require the number of clusters to be specified, which is here unknown. Let
![]() be a set of
be a set of ![]() vectors representing the images. Let
vectors representing the images. Let
![]() represents prototypes of the
represents prototypes of the ![]() clusters. CA minimizes the following objective function:
clusters. CA minimizes the following objective function:
In (1),
![]() stands for the distance from an image signature
stands for the distance from an image signature ![]() to a cluster prototype
to a cluster prototype ![]() (for spherical clusters, Euclidean distance will be used) and
(for spherical clusters, Euclidean distance will be used) and ![]() is the membership of
is the membership of ![]() to a cluster
to a cluster ![]() . The first term is the standard FCM objective function [1]: the sum of weighted square distances. The second term leads to reduce the number of clusters. By minimizing both terms simultaneously, the data set will be partitioned in the optimal number of clusters while clusters will be arranged in order to minimize the sum of intra-cluster distances.
. The first term is the standard FCM objective function [1]: the sum of weighted square distances. The second term leads to reduce the number of clusters. By minimizing both terms simultaneously, the data set will be partitioned in the optimal number of clusters while clusters will be arranged in order to minimize the sum of intra-cluster distances.
Membership can be written as:
and
where the cardinality of a cluster is defined by
![]() . The first term in equation (3) is the membership term in FCM algorithm and takes into account only relative distances to the clusters. The second term leads to a reduction of cardinality of spurious clusters, which are discarded if their cardinality drops below a threshold. So only good clusters are conserved.
. The first term in equation (3) is the membership term in FCM algorithm and takes into account only relative distances to the clusters. The second term leads to a reduction of cardinality of spurious clusters, which are discarded if their cardinality drops below a threshold. So only good clusters are conserved.
![]() should provide a balance [5] between the two terms of (1), so
should provide a balance [5] between the two terms of (1), so ![]() at iteration
at iteration ![]() is defined by :
is defined by :
The exponential factor makes the second term preponderant in a first time to reduce the number of cluster, and then the first term dominates to seek the best partition of the data.
Adaptive Robust Competition (ARC)
Dimensionality Reduction
We have computed a signature space for the Columbia Object Image Library [9] (a 1440 gray scale image database representing 20 objects shot every 5 degrees). This feature space is high-dimensional and contains three signatures:- Intensity distribution (16-D): the gray level histogram.
- Texture (8-D): the Fourier power spectrum is used to describe the spatial frequency of the image [10].
- Shape and Structure (128-D): the correlogram of edge-orientations histogram (in the same way as color correlogram presented at [7]).
To prevent the clustering to be computationally expensive, a principal component analysis is performed to reduce the dimensionality. For each feature, only the first principal components are kept.
Adaptive Competition
Since clusters have different compacities, the problem is to attenuate the effect of ![]() for loose clusters, in order to not discard them too rapidly. We introduce an average distance for each cluster
for loose clusters, in order to not discard them too rapidly. We introduce an average distance for each cluster ![]() :
:
Then,
The ratio
Robust clustering
A solution to deal with outliers and data points with ambiguous memberships is to capture such signatures in a single cluster [3]. Let this noise cluster be the first cluster, and let define a virtual noise prototype ![]() such as:
such as:
Then the objective function (1) has to be minimized under the following constraint:
- Distances for the good clusters
 are defined by:
are defined by:
where are positive definite matrices. If
are positive definite matrices. If  are identity matrices, then the distance is Euclidean distance, and the prototypes of clusters
are identity matrices, then the distance is Euclidean distance, and the prototypes of clusters  are:
are:
- For the noise cluster
 , distance is given by (10).
, distance is given by (10).
The noise distance ![]() is computed as the average of distances between image signatures and good cluster prototypes:
is computed as the average of distances between image signatures and good cluster prototypes:
Choice of distance for good clusters
What would be the most appropriate choice for (11) ? The image signatures are composed of different features which describe different attributes. The distance between signatures is defined as the weighted sum of partial distances for each feature
![]() :
:
Since the natural categories in image databases have various shapes (the more often hyper-ellipsoidal) and are overlapping, Euclidean distance is not appropriate. So the Mahalanobis distance [6] is used to discriminate image signatures. For clusters
![]() , partial distances for feature
, partial distances for feature ![]() are computed using:
are computed using:
Normalization of features
The features have different orders of magnitude and different dimensions, so the distance cannot be a simple sum of partial distances. The idea is to learn the weights ![]() in equation (14) during the clustering process. Ordered Weight Averaging [12] is used, as proposed in [4].
in equation (14) during the clustering process. Ordered Weight Averaging [12] is used, as proposed in [4].
First, partial distances are sorted in ascending order. For each feature ![]() , the average rank of corresponding partial distance over images is obtained:
, the average rank of corresponding partial distance over images is obtained:
In this process: 1) Features are normalized. 2) Similar images according to a single feature (i.e. which have a small partial distance) are clustered together since the weight of this feature will be increased.
Algorithm outline
- Fix the maximum number of clusters
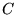 .
.
- Initialize randomly prototypes for
 .
.
- Initialize memberships with equal probability for each image to belong to each cluster.
- Initialize feature weights uniformly for each cluster
 .
.
- Compute initial cardinalities for
 .
.
- Repeat
- Compute covariance matrix for
 and feature subsets
and feature subsets  using (16).
using (16).
- Compute
 using (10) for
using (10) for  and (15) for
and (15) for  .
.
- Update weights for clusters
 using (18) for each feature.
using (18) for each feature.
- Compute
 for
for  using equations (9) and (6).
using equations (9) and (6).
- Compute memberships
 using equation (3) for each cluster and each signature.
using equation (3) for each cluster and each signature.
- Compute cardinalities
 for
for  .
.
- For
 , if
, if
 discard cluster
discard cluster  .
.
- Update number of clusters
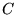 .
.
- Update the prototypes using equation (12).
- Update noise distance
 using equation (13).
using equation (13).
- Compute covariance matrix for
- Until (prototypes stabilize).
Results and discussion
ARC is compared to two other clustering algorithms: the basic CA algorithm presented in §2 and the Self-Organization of Oscillator Network (SOON) algorithm [4].
The categorization is performed on the three features. For each category, a prototype is chosen according to the following steps: First, the average value of each feature is computed over image; Then the average of all images defines a virtual prototype; The real prototype is the nearest image to the virtual one.
The three summaries are presented on figures (1), (2) and (3). Almost all the natural categories are retrieved with the three methods. But with SOON or CA algorithms, some categories are split in several clusters, so prototypes are redundant. Our method provides a better summary with less redundancy.
Then, since the CA algorithm has no cluster to collect ambiguous image signatures, the clusters are noisy. With both ARC and SOON algorithms, noise signatures are put in a separate cluster, so clusters considered as good have quite no noise. With the SOON algorithm, more than one quarter of the database is considered as noise (table 1). It leads to have really good (i.e. without noise) clusters, but the drawback is that cluster are small, and contain not more than the third of the natural category: so they do not provide a good representation of the database. Our method puts only the ambiguous images in the noise cluster, and finds almost all the images of the natural category.
| ARC | SOON | CA | |
| mass of mis-categorized images | |||
| noise cluster mass |
Conclusion
We have presented a new unsupervised and adaptive clustering algorithm to categorize image databases. When prototypes of each category are picked and collected together, it provides a summary for the image database. It allows to face the problems raised by image database browsing and more specifically handle the ``page zero'' one. It allows to compute the optimal number of clusters in the data-set. It collects outliers and ambiguous image signatures in a noise cluster, to prevent them from biasing the categorization process. Finally, it uses an appropriate distance to retrieve clusters of various shapes and densities.
Bibliography
-
- 1
- J. C. Bezdek.
Pattern Recognition with Fuzzy Objective Function Algorithms.
Plenum Press, 1981.- 2
- N. Boujemaa.
On competitive unsupervized clustering.
In Proc. of ICPR'2000, Barcelona, Spain.- 3
- R. N. Dave.
Characterization and detection of noise in clustering.
Pattern Recognition Letters, 12, 1991.- 4
- H. Frigui, N. Boujemaa, and S.-A. Lim.
Unsupervised clustering and feature discrimination with application to image database categorization.
In NAFIPS, Vancouver, Canada, 2001.- 5
- H. Frigui and R. Krishnapuram.
Clustering by competitive agglomeration.
Pattern Recognition, 30(7), 1997.- 6
- E. E. Gustafson and W. C. Kessel.
Fuzzy clustering with a fuzzy covariance matrix.
In IEEE CDC, San Diego, California, 1979.- 7
- J. Huang, S. R. Kumar, M. M, and Z. W.-J.
Spatial color indexing and applications.
In ICCV, Bombay, India, 1998.- 8
- S. Medasani and R. Krishnapuram.
Categorization of image databases for efficient retrieval using robust mixture decomposition.
In IEEE CBAIVL'1998, Santa Barbara, California.- 9
- S. A. Nene, S. K. Nayar, and H. Murase.
Columbia object image library (coil-20).
Technical report, Columbia University, http://www.cs.columbia.edu/CAVE/, 1996.- 10
- H. Niemann.
Pattern Analysis and Understanding.
Springer, Heidelberg, 1990.- 11
- J. Z. Wang, G. Wiederhold, O. Firschein, and S. X. Wei.
Content-based image indexing and searching using daubechies' wavelets.
Int. J. on Digital Libraries, 1(4), 1997.- 12
- R. R. Yager.
On ordered weighted averaging aggregation operators in multicriteria decision making.
Systems, Man and Cybernetics, 18(1), 1988.
![\begin{displaymath}
J = \sum_{j=1}^C \sum_{i=1}^N (u_{ji})^2 d^2(x_i, \beta_j) - \alpha \sum_{j=1}^C \Big[ \sum_{i=1}^N (u_{ji}) \Big]^2
\end{displaymath}](img5.png)

![\begin{displaymath}
u_{st}^{FCM} = \frac{[1/d^2(x_t, \beta_s)]}{\sum_{j=1}^C {[1/d^2(x_t, \beta_j)]}},
\end{displaymath}](img13.png)
![\begin{displaymath}
u_{st}^{Bias} = \frac{\alpha}{d^2(x_t, \beta_s)}
\big( N_s ...
..., \beta_j)] N_j} }
{\sum_{j=1}^C {1/d^2(x_t, \beta_j)}}
\big)
\end{displaymath}](img14.png)
![\begin{displaymath}
\alpha(k) = \eta_0 \exp(-k/\tau)
\frac{\sum_{j=1}^C {\sum_{...
...\beta_j)}}
{\sum_{j=1}^C \Big[ \sum_{i=1}^N (u_{ji}) \Big]^2}
\end{displaymath}](img18.png)
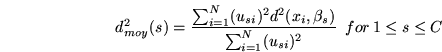






![\includegraphics[width=\textwidth]{col_proto_ridc.eps}](img64.png)
![\includegraphics[width=\textwidth]{col_proto_soon.eps}](img65.png)
![\includegraphics[width=\textwidth]{col_proto_ca.eps}](img66.png)